R libraries

Install, if necessary, and load necessary libraries and set up R session. If you are running the docker container or using an instance on the orchestra platform, then you should have these libraries installed already.

#if (!requireNamespace("BiocManager", quietly = TRUE)) #install.packages("BiocManager")
library(magrittr)
library(ade4)
library(FactoMineR)
library(factoextra)
library(ggplot2)

PCA in R

In R, there are several functions in many different packages that allow us to perform PCA. We will not review all of these, however will provide examples of the following;

svd() (stats) ** on centered data**
prcomp() (stats)
princomp() (stats) ** on cor matrix **
PCA() (FactoMineR)
dudi.pca() (ade4)

Note, although prcomp sets scale=FALSE for consistency with S, in general scaling is advised. We will demonstrate both prcomp of unscaled and scaled data. Scaling the variables to have unit variance is advised.

Give an input matrix, P and a resulting output, res

Function	loadings	scores	plot
`prcomp(P, center=TRUE, scale=TRUE`)	`res$rotation`	`res$x`	`biplot(res)`
`princomp(P, cor=TRUE)`	`res$loadings`	`res$scores`	`biplot(res)`
`PCA(P)`	`res$svd$V`	`res$ind$coord`	`plot(res)`
`dudi.pca(P, center=TRUE, scale=TRUE)`	`res$c1`	`res$li`	`scatter(res)`

With ade4::dudi.pca and prcomp the default is center = TRUE, scale = TRUE.

With princomp, cor=FALSE is the default.

A simple toy dataset

We will demonstrate some of these and how the methods relate but first we will create a simple minimal cloud of points; two vectors, x,y of length 100.

 set.seed(2)             #sets the seed for random number generation.
 x <- 1:100              #creates a vector x with numbers from 1 to 100
 ex <- rnorm(100, 0, 30) #100 normally distributed random numbers, mean=0, sd=30
 ey <- rnorm(100, 0, 30) # 100 normally distributed random numbers, mean=0, sd=30
 y <- 30 + 2 * x         #sets y to be a vector that is a linear function of x
 x_obs <- x + ex         #adds "noise" to x
 y_obs <- y + ey         #adds "noise" to y
 
# Bind both vectors in a matrix of toy data called P
P <- data.frame(x_obs=x_obs,y_obs=y_obs) #places points in matrix
summary(P)

##      x_obs            y_obs       
##  Min.   :-53.33   Min.   : 14.13  
##  1st Qu.: 21.44   1st Qu.: 97.22  
##  Median : 44.37   Median :134.91  
##  Mean   : 49.58   Mean   :131.88  
##  3rd Qu.: 77.91   3rd Qu.:174.29  
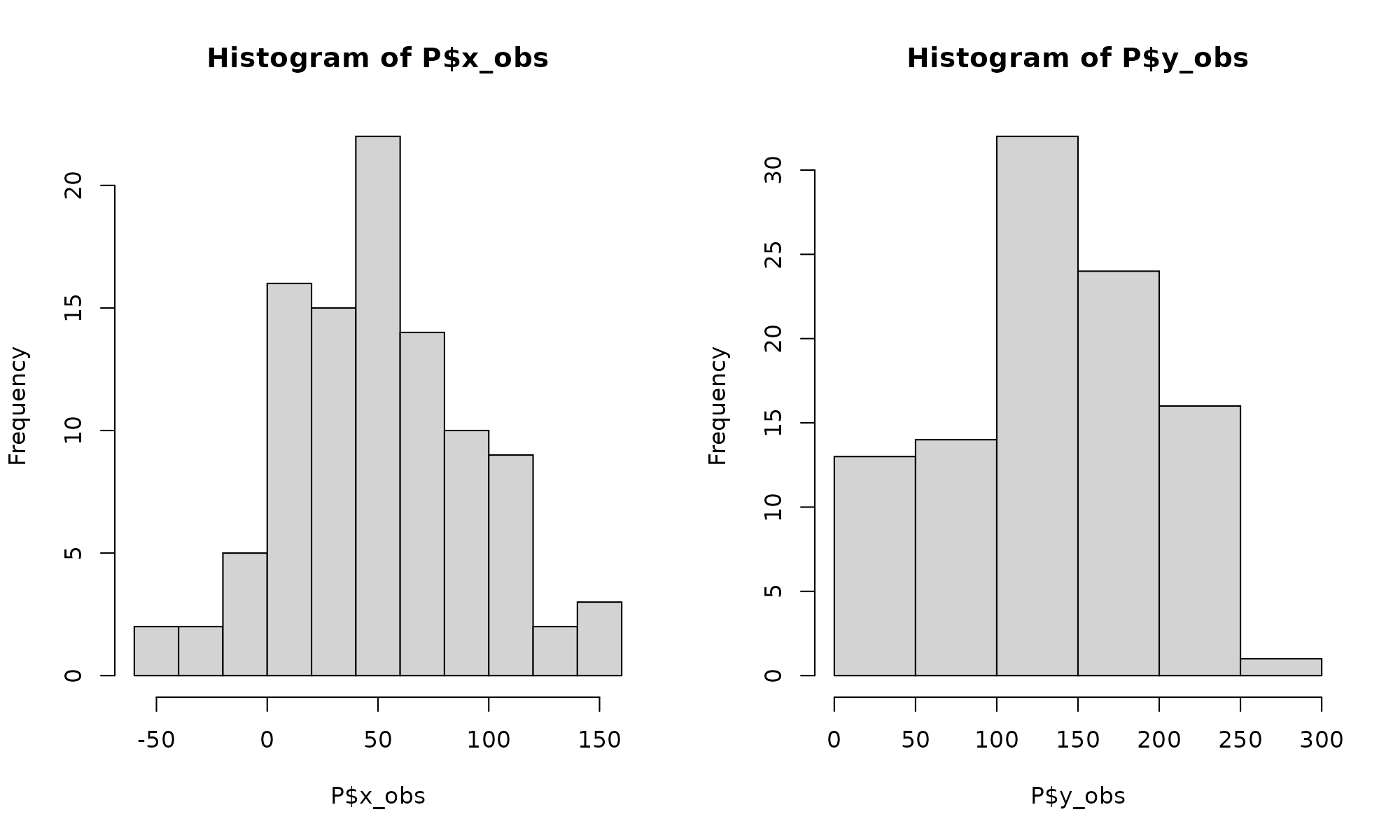
##  Max.   :155.78   Max.   :252.63

Basic histogram of the two distributions:

 par(mfrow=c(1,2))
 hist(P$x_obs)
 hist(P$y_obs)

Difference between covariance-based and correlation-based PCA

When performing PCA, you will encounter, two forms of PCA; PCA of a covariance or correlation matrix.

The difference between these is can be most easily understood in the data pre-processing. In the first vignette in this package, PCA was computed as a singular value decomposition (SVD) of a column centered, scaled matrix. This was PCA of the correlation matrix. If the matrix is centered but not scaled, it is PCA of the covariance matrix.

PCA of a correlation matrix = svd of scaled, centered, matrix (z-score matrix)

covariance-based PCA

PCA of a covariance matrix can be computed as svd of unscaled, centered, matrix

Center a matrix Recall we had two vector x_obs, y_obs. We can center these columns by subtracting the column mean from each object in the column. We can perform PCA of the covariance matrix is several ways.

SVD of the centered matrix
eigenanalysis of the centered, covariance matrix
using prcomp with scale=FALSE (which is the default)

svd of centered data.

\[\$d\] returns the singular values, not the eigenvalues.

Mx<- scale(P, center=TRUE, scale=FALSE)
(svd(Mx)$d / sqrt(max(1, c(dim(Mx)- 1))))^2

## [1] 4110.45 1189.45

Eigen on a covariance matrix

MCov <- cov(Mx) 
eigen(MCov)

## eigen() decomposition
## $values
## [1] 4110.45 1189.45
## 
## $vectors
##           [,1]       [,2]
## [1,] 0.4527354 -0.8916449
## [2,] 0.8916449  0.4527354

eigenvalues <-eigen(MCov)$values
eigenVectors<-eigen(MCov)$vectors

prcomp

This is the same as prcomp PCA of the unscaled data. By default prcomp will perform decomposition of data that is centered but not scaled (center = TRUE, scale = FALSE)

prcomp(P)

## Standard deviations (1, .., p=2):
## [1] 64.11279 34.48841
## 
## Rotation (n x k) = (2 x 2):
##             PC1        PC2
## x_obs 0.4527354 -0.8916449
## y_obs 0.8916449  0.4527354

Note that the eigenvalues are provided as;

prcomp(P)$sdev^2

## [1] 4110.45 1189.45

and this is also similar to princomp

princomp(P)$sdev^2

##   Comp.1   Comp.2 
## 4069.345 1177.556

eigenvector from the eigenanalysis of the covariance matrix equal the rotation matrix of prcomp.

print("$v right singular vectors of svd of centered matrix")

## [1] "$v right singular vectors of svd of centered matrix"

svd(Mx)$v

##           [,1]       [,2]
## [1,] 0.4527354 -0.8916449
## [2,] 0.8916449  0.4527354

print("eigen of covariance matrix")

## [1] "eigen of covariance matrix"

eigen(MCov)$vectors

##           [,1]       [,2]
## [1,] 0.4527354 -0.8916449
## [2,] 0.8916449  0.4527354

print("prcomp of centered but not scaled (default options) matrix")

## [1] "prcomp of centered but not scaled (default options) matrix"

prcomp(P)$rotation

##             PC1        PC2
## x_obs 0.4527354 -0.8916449
## y_obs 0.8916449  0.4527354

The right singular vectors are the eigenvectors of M^tM. Next I plot the principal axes (yellow):

plot(P,asp=1,col=1) #plot points
points(x=mean(x_obs),y=mean(y_obs),col="orange", pch=19) #show center
lines(x_obs,eigenVectors[2,1]/eigenVectors[1,1]*Mx[x]+mean(y_obs),col=8)

This shows the first principal axis. Note that it passes through the mean as expected. The ratio of the eigenvectors gives the slope of the axis.

Next plot the second principal axis, orthogonal to the first

plot(P,asp=1,col=1) #plot points
points(x=mean(x_obs),y=mean(y_obs),col="orange", pch=19) #show center
lines(x_obs,eigenVectors[2,1]/eigenVectors[1,1]*Mx[x]+mean(y_obs),col=8)
lines(x_obs,eigenVectors[2,2]/eigenVectors[1,2]*Mx[x]+mean(y_obs),col=8)

shows the second principal axis, which is orthogonal to the first (recall that the matrix V^t in the singular value decomposition is orthogonal). This can be checked by noting that the second principal axis is also, as the product of orthogonal slopes is -1.

Correlation-based PCA

Correlation-based PCA can be computed by singular value decomposition (svd) of centered and scaled matrix. So we can repeat the code above but scale and center the data with scale(P, center=TRUE, scale=TRUE). By default scale will center and scale

scale

## function (x, center = TRUE, scale = TRUE) 
## UseMethod("scale")
## <bytecode: 0x5558b2d38688>
## <environment: namespace:base>

svd of z-score scaled data.

p0<-svd(scale(P))
p0$d         #the singular values

## [1] 12.065827  7.239877

p0$v        #the right singular vectors

##           [,1]       [,2]
## [1,] 0.7071068 -0.7071068
## [2,] 0.7071068  0.7071068

Recall, SVD returns a list with components

d = a vector containing the singular values of x, of length min(n, p), in descending order

u = a matrix whose columns contain the left singular vectors of x, present if nu > 0. Dimension c(n, nu).

v = a matrix whose columns contain the right singular vectors of x, present if nv > 0. Dimension c(p, nv).

where the product of these matrix \[X = U D V'\] recovers the original matrix;

(p0$u %*% diag(p0$d) %*% t(p0$v))%>% head

##             [,1]       [,2]
## [1,] -1.78511160 -1.1414577
## [2,] -0.99401402 -1.5197211
## [3,]  0.02497959 -1.7769963
## [4,] -1.87979464 -1.9636443
## [5,] -1.11114369 -1.9868817
## [6,] -0.93661695 -0.4798394

which equals the scaled matrix that was decomposed using svd

scale(P)%>% head

##            x_obs      y_obs
## [1,] -1.78511160 -1.1414577
## [2,] -0.99401402 -1.5197211
## [3,]  0.02497959 -1.7769963
## [4,] -1.87979464 -1.9636443
## [5,] -1.11114369 -1.9868817
## [6,] -0.93661695 -0.4798394

The elements of d are formed by taking the sum of the squares of the principal components but not dividing by the rank. Therefore we can divide by the rank, which is user-defined or min of the ncol or nrow of the matrix -1.

The diagonal elements of d from the SVD are proportional to the standard deviations (sdev) returned by PCA.

p0$d^2/(nrow(p0$u) - 1)

## [1] 1.4705472 0.5294528

eigenValues= p0$d^2/(nrow(p0$u) - 1)
eigenValues

## [1] 1.4705472 0.5294528

Summary of output from svd

svdSummary<-function(svdRes,sf=4){
  if(is(svdRes,"prcomp")){
    eigenvalue=svdRes$sdev^2
  }else{
  #d=signif(svdRes$d,sf)
  eigenvalue= svdRes$d^2/(nrow(svdRes$u) - 1)
}
  data.frame(cbind(
  eigenvalues=signif(eigenvalue,sf),
  sd = signif(sqrt(eigenvalue),sf),
  variance.percent = paste0(signif((eigenvalue/sum(eigenvalue)),2)*100,"%"),
  cumulative.variance.percent = paste0(cumsum(signif((eigenvalue/sum(eigenvalue)),2))*100,"%")))
}


eigSum.svd <-svdSummary(p0)
eigSum.svd

##   eigenvalues     sd variance.percent cumulative.variance.percent
## 1       1.471  1.213              74%                         74%
## 2      0.5295 0.7276              26%                        100%

prcomp (scale = TRUE)

First stats::prcomp. The eigenvectors are stored in $rotation. Note these are the same as svd$v on scale data

p1<- prcomp(P, scale = TRUE)
p1$rotation

##             PC1        PC2
## x_obs 0.7071068 -0.7071068
## y_obs 0.7071068  0.7071068

 (p1$rotation== p0$v)

##        PC1  PC2
## x_obs TRUE TRUE
## y_obs TRUE TRUE

eigenvalues - $sdev eigenvector - $rotation

names(p1)

## [1] "sdev"     "rotation" "center"   "scale"    "x"

summary(p1)

## Importance of components:
##                           PC1    PC2
## Standard deviation     1.2127 0.7276
## Proportion of Variance 0.7353 0.2647
## Cumulative Proportion  0.7353 1.0000

To calculated eigenvalues information manually here is the code;

sf=4
eigs= p1$sdev^2
eigSum.pca= cbind(
  eigenvalue=eigs,
  sd = sqrt(eigs),
  variance.percent = eigs/sum(eigs),
  cumulative.variance.percent = cumsum(eigs)/sum(eigs))

eigSum.pca

##      eigenvalue       sd variance.percent cumulative.variance.percent
## [1,]  1.4705472 1.212661        0.7352736                   0.7352736
## [2,]  0.5294528 0.727635        0.2647264                   1.0000000

which is the same as;

eigSum.svd

##   eigenvalues     sd variance.percent cumulative.variance.percent
## 1       1.471  1.213              74%                         74%
## 2      0.5295 0.7276              26%                        100%

If we had more components, we could generate a scree plot. Its not very useful with 2 components, but here is the code

Caculate the Proportion of Variance explained by each component (eig sum Proportion above)

ProportionVariance = p0$d^2 /sum(p0$d^2 )
ProportionVariance

## [1] 0.7352736 0.2647264

plot(ProportionVariance, xlim = c(0, 5), type = "b", pch = 16, xlab = "principal components", 
    ylab = "variance explained")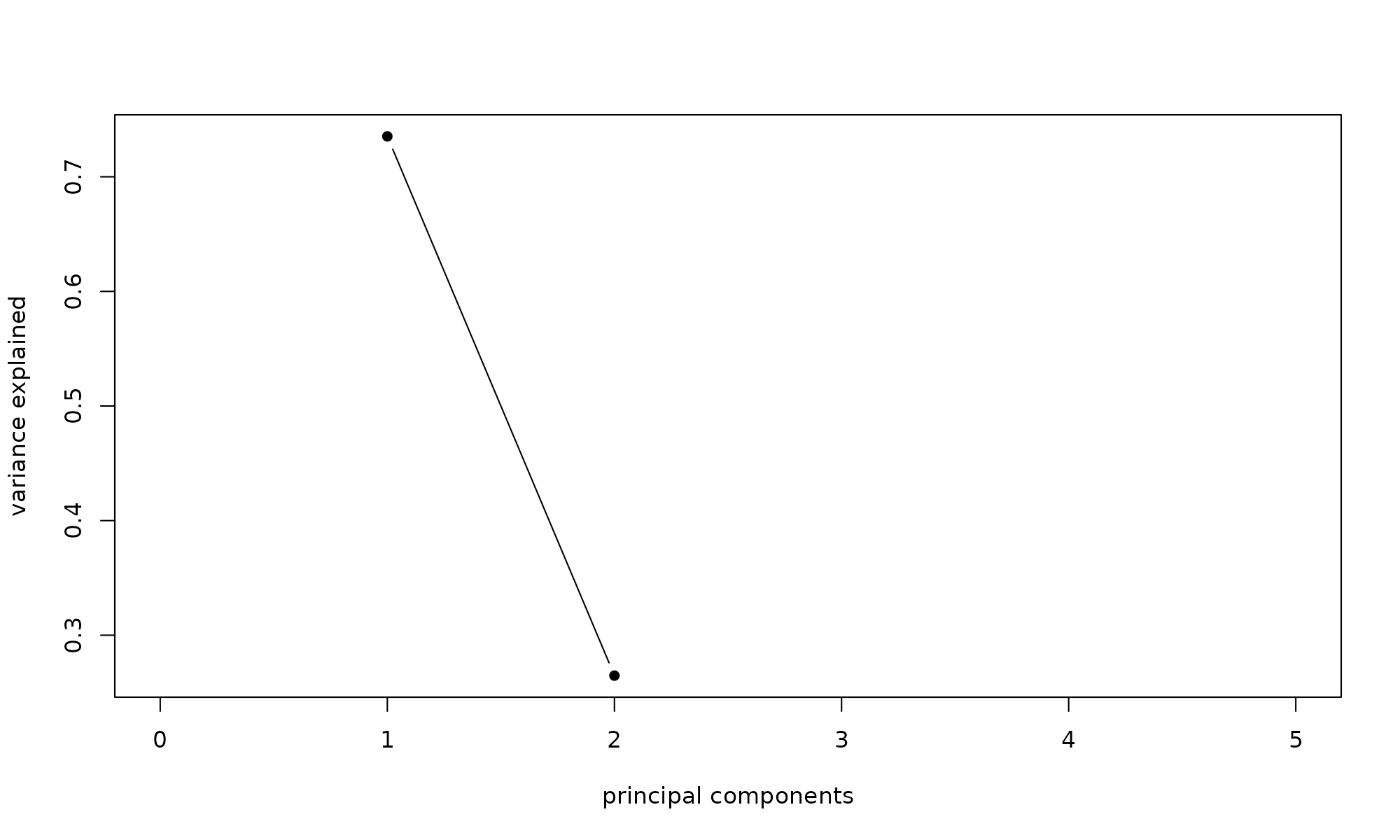

`princomp`

princomp was written for compatiblity with S-PLUS however it is not recommended. Its is better to use prcomp or svd. That is because by default princomp performs a decompostion of the covariance not correlation matrix. princomp can call eigen on the correlation or covariance matrix. Its default calculation uses divisor N for the covariance matrix.

p2<-stats::princomp(P)
p2$sd^2

##   Comp.1   Comp.2 
## 4069.345 1177.556

sqrt of eigenvalues

p2$sdev

##   Comp.1   Comp.2 
## 63.79142 34.31553

eigenvectors

p2$loadings

## 
## Loadings:
##       Comp.1 Comp.2
## x_obs  0.453  0.892
## y_obs  0.892 -0.453
## 
##                Comp.1 Comp.2
## SS loadings       1.0    1.0
## Proportion Var    0.5    0.5
## Cumulative Var    0.5    1.0

head(p2$scores,2)

##         Comp.1     Comp.2
## [1,] -94.48864 -36.682917
## [2,] -99.33030   3.293649

Set cor = TRUE in the call to princomp in order to perform PCA on the correlation matrix (instead of the covariance matrix)

p2b<-princomp(P, cor = TRUE)
p2b$sdev^2

##    Comp.1    Comp.2 
## 1.4705472 0.5294528

p2b$loadings

## 
## Loadings:
##       Comp.1 Comp.2
## x_obs  0.707  0.707
## y_obs  0.707 -0.707
## 
##                Comp.1 Comp.2
## SS loadings       1.0    1.0
## Proportion Var    0.5    0.5
## Cumulative Var    0.5    1.0

For more info on prcomp v princomp see http://www.sthda.com/english/articles/31-principal-component-methods-in-r-practical-guide/118-principal-component-analysis-in-r-prcomp-vs-princomp/

`FactoMineR`

FactoMineR::PCA calls svd to compute the PCA

p3<-FactoMineR::PCA(P)

The eigenvalues, same as eigSum and eigSum.svd above

t(p3$eig)

##                                      comp 1      comp 2
## eigenvalue                         1.470547   0.5294528
## percentage of variance            73.527362  26.4726382
## cumulative percentage of variance 73.527362 100.0000000

correlations between variables and PCs

p3$var$coord

##          Dim.1      Dim.2
## x_obs 0.857481  0.5145157
## y_obs 0.857481 -0.5145157

`ade4::dudi.pca`

First ade4::dudi.pca scales the data and stores the scaled data in $tab. In PCA this will be almost equivalent to scale. However there is a minor difference (see https://pbil.univ-lyon1.fr/R/pdf/course2.pdf). ade4 uses the duality diagram framework for computing pca and other matrix factorizations (so it provides lw and cw which are the row and columns weights, respectively). See Cruz and Holmes 2011 for a wonderful tutorial on the duality diagram framework https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3265363/

p4<-ade4::dudi.pca(P, scannf = FALSE, nf=2)  # save 2 axis by default,
head(p4$tab)  # centered/scaled data.

##         x_obs      y_obs
## 1 -1.79410466 -1.1472082
## 2 -0.99902168 -1.5273772
## 3  0.02510543 -1.7859484
## 4 -1.88926469 -1.9735368
## 5 -1.11674143 -1.9968913
## 6 -0.94133545 -0.4822568

head(scale(P))

##            x_obs      y_obs
## [1,] -1.78511160 -1.1414577
## [2,] -0.99401402 -1.5197211
## [3,]  0.02497959 -1.7769963
## [4,] -1.87979464 -1.9636443
## [5,] -1.11114369 -1.9868817
## [6,] -0.93661695 -0.4798394

The values used for centering are stored in cent, it is equal to the colMeans. norm provides the sd of the columns

p4$cent == colMeans(P)

## x_obs y_obs 
##  TRUE  TRUE

sd.n <- function(x) sqrt(var(x) * (length(x) - 1)/length(x))
identical(p4$norm,apply(P, 2, sd.n))

## [1] TRUE

The summary printout is equivalent to P3 (p3$eig) above. The eigenvales are stored in p4$eig.

summary(p4)

## Class: pca dudi
## Call: ade4::dudi.pca(df = P, scannf = FALSE, nf = 2)
## 
## Total inertia: 2
## 
## Eigenvalues:
##     Ax1     Ax2 
##  1.4705  0.5295 
## 
## Projected inertia (%):
##     Ax1     Ax2 
##   73.53   26.47 
## 
## Cumulative projected inertia (%):
##     Ax1   Ax1:2 
##   73.53  100.00

p4$eig

## [1] 1.4705472 0.5294528

p4$c1

##             CS1        CS2
## x_obs 0.7071068 -0.7071068
## y_obs 0.7071068  0.7071068

p4$co

##          Comp1      Comp2
## x_obs 0.857481 -0.5145157
## y_obs 0.857481  0.5145157

The cumulative % of variance explained by each component:

(k <- 100 * p4$eig/sum(p4$eig))

## [1] 73.52736 26.47264

cumsum(k)

## [1]  73.52736 100.00000

nf is an integer giving the number of axes kept. nf will always be smaller than the smaller of: the number of rows or number of columns of the matrix; minus 1.

p4$nf

## [1] 2

c1 gives the variables’ coordinates, normed to 1. It is also called the coefficients of the combination or the loadings of variables.

Equally, the output matrix l1 gives the individuals’ coordinates, normed to 1. It is also called the loadings of individuals.

p4$c1

##             CS1        CS2
## x_obs 0.7071068 -0.7071068
## y_obs 0.7071068  0.7071068

sum(p4$cw * p4$c1$CS1^2)

## [1] 1

co gives the variables’ coordinates, normed to the square root of the eigenvalues.

p4$co

##          Comp1      Comp2
## x_obs 0.857481 -0.5145157
## y_obs 0.857481  0.5145157

sum(p4$cw * p4$co$Comp1^2)

## [1] 1.470547

The link between c1 and co is defined by:

p4$c1$CS1 * sqrt(p4$eig[1])

## [1] 0.857481 0.857481

Comparision of results of these different PCA methods

There is also a nice package called factoextra. This works all of the above classes

library(factoextra)

res<- list(p0,p1,p2,p2b,p3,p4) 
names(res) = c('svd_scaledData','prcomp', 'princomp','princomp_cov', 'FactoMineR', 'ade4')

e<-sapply(res[-1],get_eig)

# get_eig doesn't work on svd
svd.e<- eigSum.svd[c(1,3,4)]

colnames(svd.e)<- names(e[[1]])


e<- c(list(svd=svd.e),e)

e

## $svd
##   eigenvalue variance.percent cumulative.variance.percent
## 1      1.471              74%                         74%
## 2     0.5295              26%                        100%
## 
## $prcomp
##       eigenvalue variance.percent cumulative.variance.percent
## Dim.1  1.4705472         73.52736                    73.52736
## Dim.2  0.5294528         26.47264                   100.00000
## 
## $princomp
##       eigenvalue variance.percent cumulative.variance.percent
## Dim.1   4069.345         77.55712                    77.55712
## Dim.2   1177.556         22.44288                   100.00000
## 
## $princomp_cov
##       eigenvalue variance.percent cumulative.variance.percent
## Dim.1  1.4705472         73.52736                    73.52736
## Dim.2  0.5294528         26.47264                   100.00000
## 
## $FactoMineR
##       eigenvalue variance.percent cumulative.variance.percent
## Dim.1  1.4705472         73.52736                    73.52736
## Dim.2  0.5294528         26.47264                   100.00000
## 
## $ade4
##       eigenvalue variance.percent cumulative.variance.percent
## Dim.1  1.4705472         73.52736                    73.52736
## Dim.2  0.5294528         26.47264                   100.00000

Visualization and Exploration of results

The github package explor is useful for exploring data. It includes plotting functions for many packages including ade4, FactoMineR and base R functions prcomp and princomp;

For now on, it is usable the following types of analyses :

Analysis	Function	Package	Notes
Principal Component Analysis	PCA	FactoMineR	-
Correspondance Analysis	CA	FactoMineR	-
Multiple Correspondence Analysis	MCA	FactoMineR	-
Principal Component Analysis	dudi.pca	ade4	Qualitative supplementary variables are ignored
Correspondance Analysis	dudi.coa	ade4	-
Multiple Correspondence Analysis	dudi.acm	ade4	Quantitative supplementary variables are ignored
Specific Multiple Correspondance Analysis	speMCA	GDAtools	Supplementary variables are not supported
Multiple Correspondance Analysis	mca	MASS	Quantitative supplementary variables are not supported
Principal Component Analysis	princomp	stats	Supplementary variables are ignored
Principal Component Analysis	prcomp	stats	Supplementary variables are ignored

#if(!"explor" %in% rownames(installed.packages()))    #devtools::install_github("juba/explor")

#if(!"scatterD3" %in% rownames(installed.packages())) 
#devtools::install_github("juba/scatterD3")

require(explor)
explor::explor(p4)

data(children)
res.ca <- CA(children, row.sup = 15:18, col.sup = 6:8)
explor(res.ca)

`factoextra`

Plotting using factoextra

library(factoextra)

fviz_eig(p1)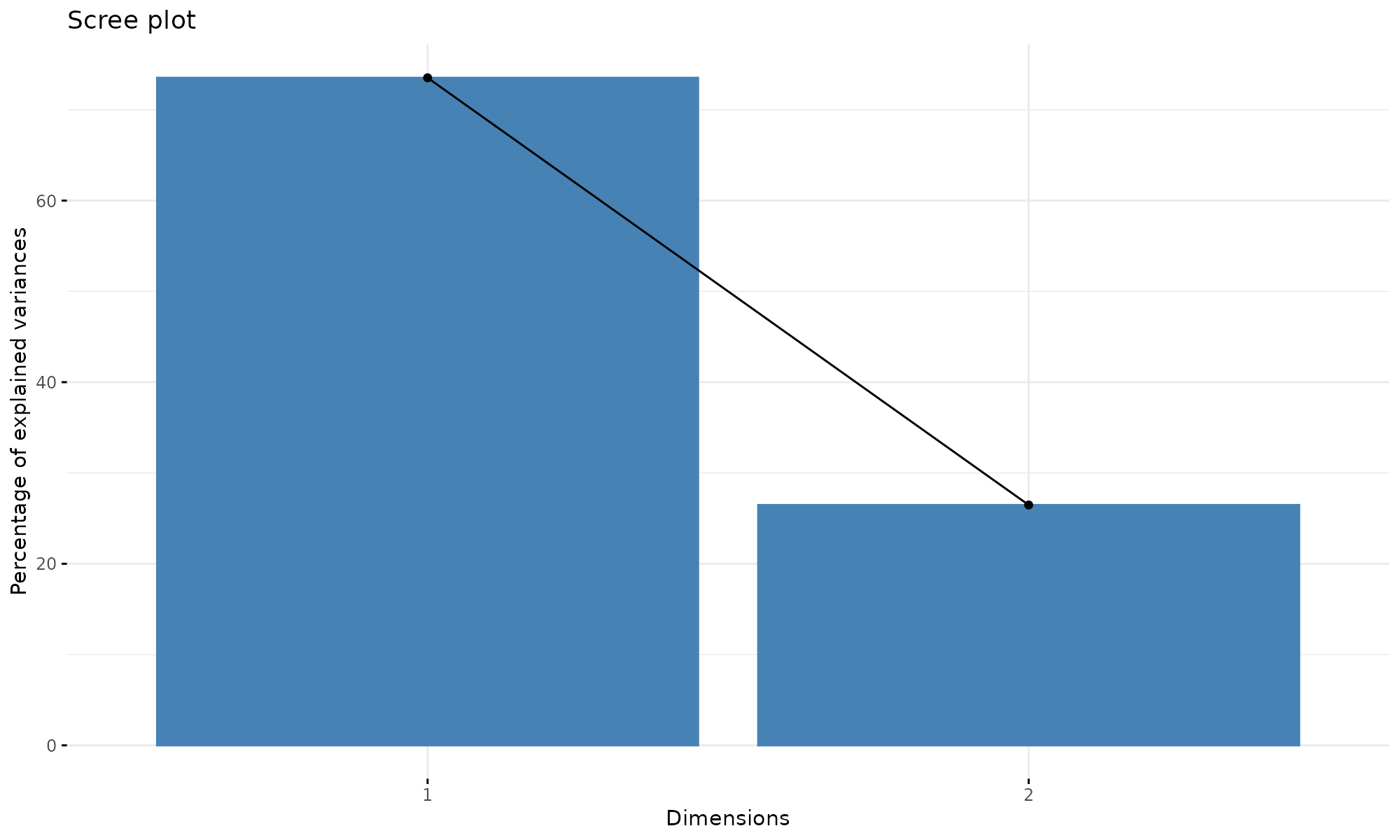

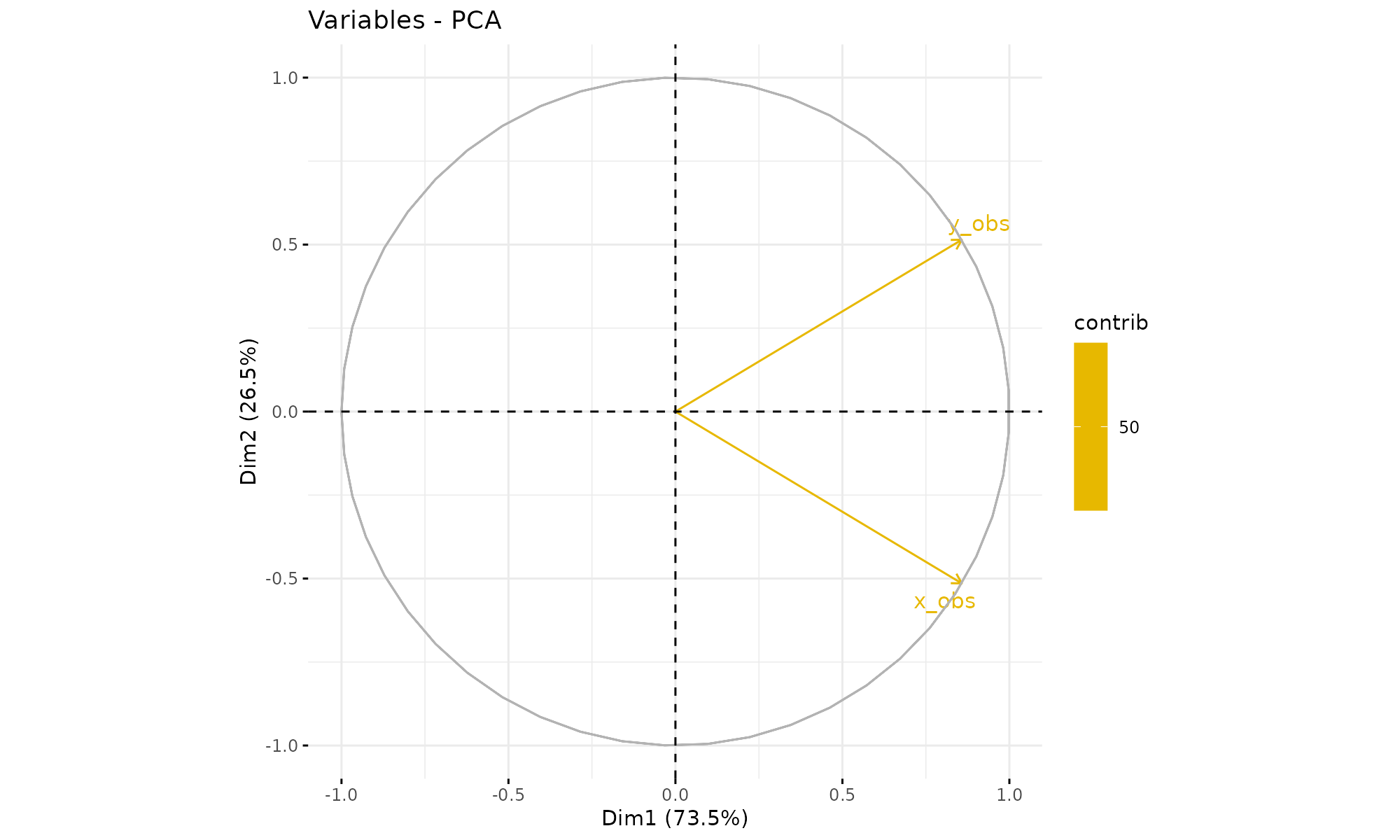
fviz_pca_var(p1,
             col.var = "contrib", # Color by contributions to the PC
             gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
             repel = TRUE     # Avoid text overlapping
             )

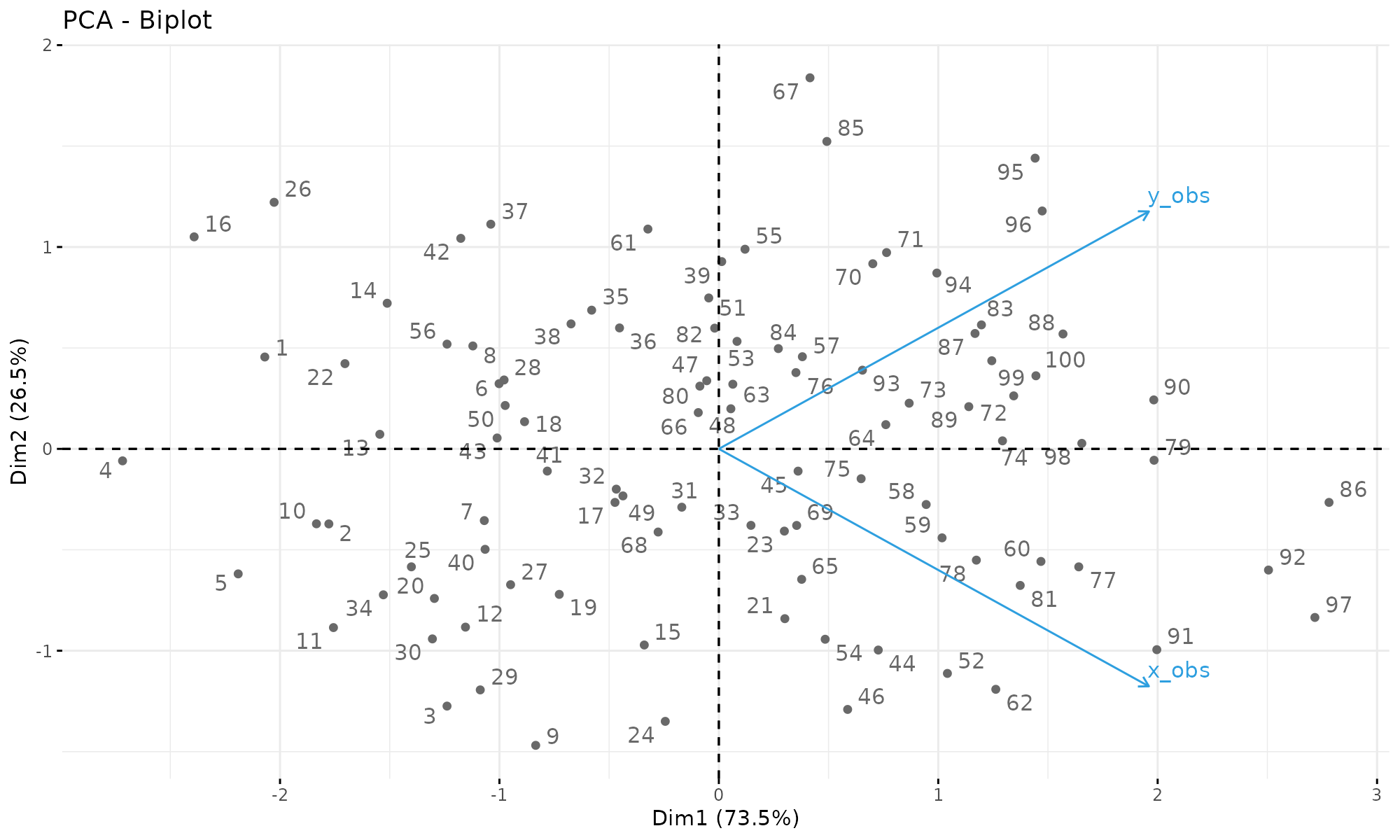
fviz_pca_biplot(p1, repel = TRUE,
                col.var = "#2E9FDF", # Variables color
                col.ind = "#696969"  # Individuals color
                )

Drawing Ellispe

Example using iris dataset

data(iris)
ir.pca<-prcomp(log(iris[,1:4]), center=TRUE, scale=TRUE)

Easiest approach:

library(ggplot2)
library(ggfortify)
ggplot2::autoplot(ir.pca, data=iris, colour="Species", frame=TRUE, frame.type="t")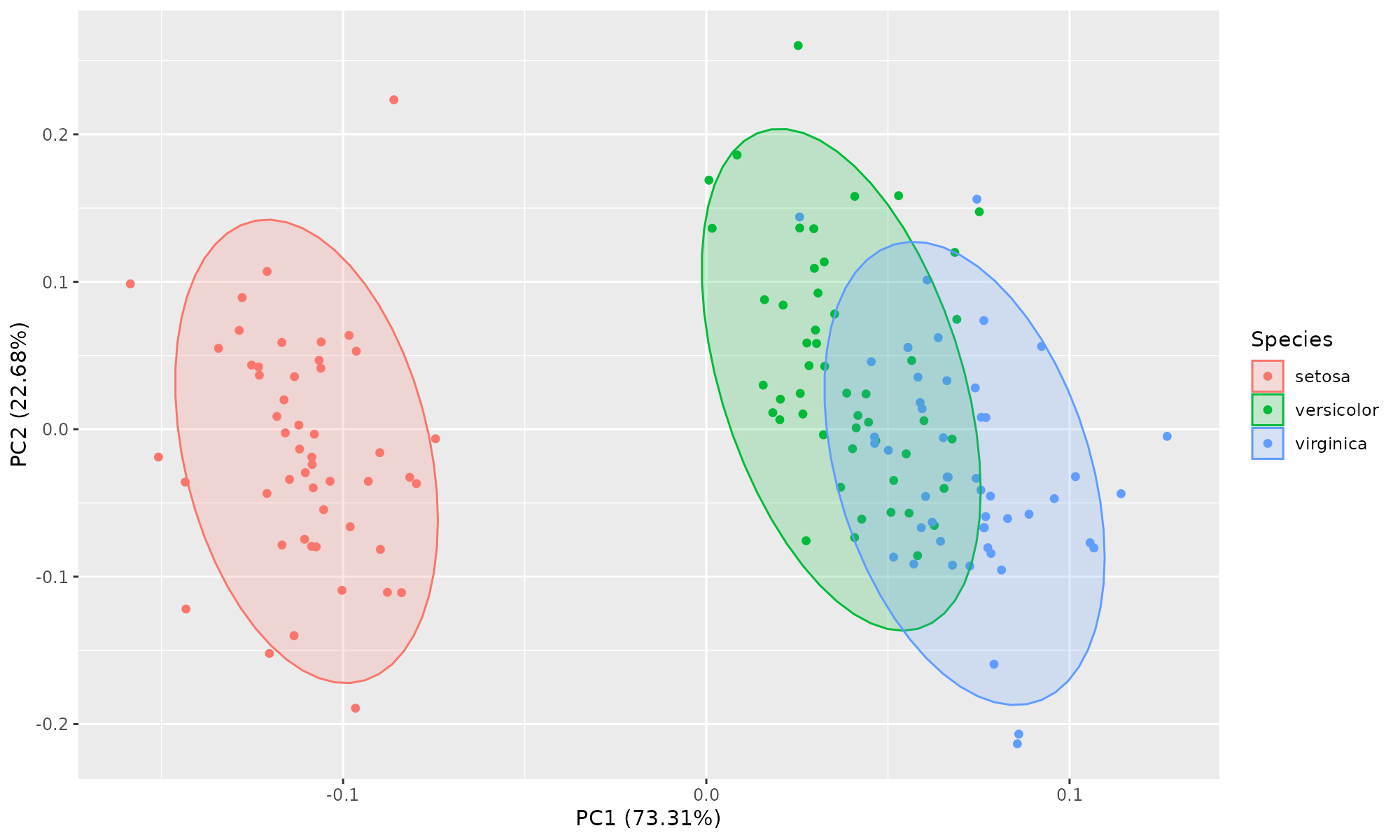

library(ggplot2)
ggplot(ir.pca,aes(PC1, PC2))+ 
  geom_point() + 
  stat_density_2d(aes(alpha=..level.., fill=iris$Species), bins=4, geom="polygon")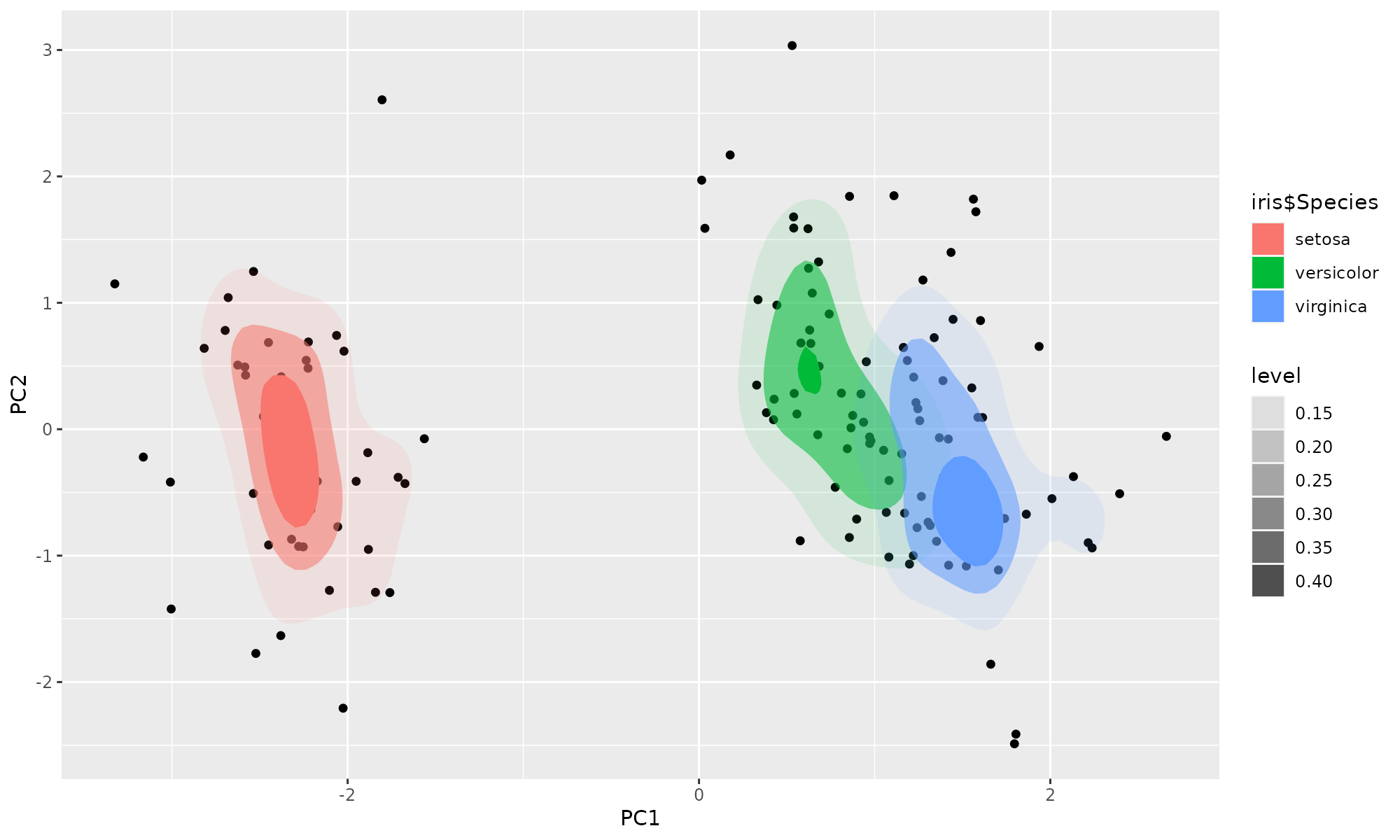

stat_ellipse() and stat_density_2d() have a lot of options. See manual pages

multivariate normal distribution.

stat_ellipse(type = "norm", linetype = 2)

Euclid, is a circle with radius equal to the level parameter

stat_ellipse(type = "euclid", level = 3)

multivariate t-distribution

stat_ellipse(type = "t")

sessionInfo()

## R version 4.1.0 (2021-05-18)
## Platform: x86_64-pc-linux-gnu (64-bit)
## Running under: Ubuntu 20.04.2 LTS
## 
## Matrix products: default
## BLAS/LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.8.so
## 
## locale:
##  [1] LC_CTYPE=en_US.UTF-8       LC_NUMERIC=C              
##  [3] LC_TIME=en_US.UTF-8        LC_COLLATE=en_US.UTF-8    
##  [5] LC_MONETARY=en_US.UTF-8    LC_MESSAGES=C             
##  [7] LC_PAPER=en_US.UTF-8       LC_NAME=C                 
##  [9] LC_ADDRESS=C               LC_TELEPHONE=C            
## [11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=C       
## 
## attached base packages:
## [1] stats     graphics  grDevices utils     datasets  methods   base     
## 
## other attached packages:
## [1] ggfortify_0.4.12 factoextra_1.0.7 ggplot2_3.3.5    FactoMineR_2.4  
## [5] ade4_1.7-17      magrittr_2.0.1   knitr_1.33      
## 
## loaded via a namespace (and not attached):
##  [1] sass_0.4.0           tidyr_1.1.3          jsonlite_1.7.2      
##  [4] carData_3.0-4        bslib_0.2.5.1        assertthat_0.2.1    
##  [7] highr_0.9            cellranger_1.1.0     yaml_2.2.1          
## [10] ggrepel_0.9.1        pillar_1.6.2         backports_1.2.1     
## [13] lattice_0.20-44      glue_1.4.2           digest_0.6.27       
## [16] ggsignif_0.6.2       colorspace_2.0-2     htmltools_0.5.1.1   
## [19] pkgconfig_2.0.3      broom_0.7.9          haven_2.4.3         
## [22] purrr_0.3.4          scales_1.1.1         openxlsx_4.2.4      
## [25] rio_0.5.27           tibble_3.1.3         generics_0.1.0      
## [28] farver_2.1.0         car_3.0-11           ellipsis_0.3.2      
## [31] ggpubr_0.4.0         DT_0.18              cachem_1.0.5        
## [34] withr_2.4.2          readxl_1.3.1         crayon_1.4.1        
## [37] memoise_2.0.0        evaluate_0.14        fs_1.5.0            
## [40] fansi_0.5.0          MASS_7.3-54          rstatix_0.7.0       
## [43] forcats_0.5.1        foreign_0.8-81       textshaping_0.3.5   
## [46] tools_4.1.0          data.table_1.14.0    hms_1.1.0           
## [49] lifecycle_1.0.0      stringr_1.4.0        munsell_0.5.0       
## [52] cluster_2.1.2        zip_2.2.0            isoband_0.2.5       
## [55] flashClust_1.01-2    compiler_4.1.0       pkgdown_1.6.1       
## [58] jquerylib_0.1.4      systemfonts_1.0.2    rlang_0.4.11        
## [61] grid_4.1.0           htmlwidgets_1.5.3    leaps_3.1           
## [64] labeling_0.4.2       rmarkdown_2.9        gtable_0.3.0        
## [67] abind_1.4-5          DBI_1.1.1            curl_4.3.2          
## [70] R6_2.5.0             gridExtra_2.3        dplyr_1.0.7         
## [73] fastmap_1.1.0        utf8_1.2.2           rprojroot_2.0.2     
## [76] ragg_1.1.3           desc_1.3.0           stringi_1.7.3       
## [79] Rcpp_1.0.7           vctrs_0.3.8          scatterplot3d_0.3-41
## [82] tidyselect_1.1.1     xfun_0.24

Principal Component Analysis in R; PCA of covariance or correlation matrix

Aedin Culhane

July 15, 2021